Figure 1. Chavin de Huantar, Machu Picchu, and Phi.

In archaeology, context is everything. In archaeogeodesy, the entire globe is the geodetic context and monuments the world over are the archaeological context. Context is essential to understanding Chavin, Andean archaeology, and the origins of civilization. Chavin cannot be fully understood without a larger context, the cosmos. Astronomy is as integral to Chavin and many other major monuments as it is to geodesy. Without astronomy you cannot navigate or determine place on the earth.

Chavin and the Golden Mean

Chavin de Huantar and Machu Picchu present several spatial interrelationships. The golden mean ratio of their arc distance and latitude difference (arc : n-s ratio) is impressively precise. Figure 1 illustrates the relationship between the Intihuatana at Machu Picchu and the centerpoint of the circular plaza at Chavin, the discovery location of a prismatic granite monolith, the Tello Obelisk. Chavin's 21 meter in diameter sunken circular court is centered on the axis of the U-shaped Old Temple platform mound, the initial monumental construction phase at Chavin. The relationship is precise using coordinates for the quadrangular granite sculptures at the two sites, the bedrock Intihuatana at Machu Picchu (GPS by Gullberg) and the sunken circular courtyard (Google Earth centerpoint coordinate, 2016 imagery) where Julio C. Tello discovered the obelisk during excavation of the site. The original sculpture is currently displayed in the Museo Nacional de Arqueología, Antropología e Historia del Perú in Lima.

The Chavin-Machu Picchu phi relationship has phi context. In 2015, I published Golden Ratio Longitudes illustrating the golden mean longitude ratios of Newark Earthworks with six major American monument complexes: Chavin de Huantar, Machu Picchu, Chichen Itza, Poverty Point, Pachacamac, and Tiwanaku (Figure 2). The longitude differences of Chavin, Tiwanaku, and Newark's Great Circle present the phi ratio (Table 1). Machu Picchu and Chichen Itza also have phi longitude relationships with Newark Earthworks while the Chavin, Chichen Itza, and Newark longitude differences additionally represent lunar astronomy constants (discussed below). 

Golden Mean Longitude Ratios
Poverty Point - Newark Octagon - Pachacamac
Itza Castillo - Newark Octagon - Machu Picchu
Newark Great Circle - Chavin de Huantar - Tiwanaku
Figure 2. Newark Earthworks Golden Mean Longitude Ratios.

Table 1. Golden Ratio:  0.618034 : 1.0 = 1.0 : 1.618034
Chavin A - Eagle Mound - Puma Punku chhha-nccm-pupup e-w ratio @ chhha = 1.0 : 0.618088 Figure 3. Phi Longitude Ratios. Screen capture from archaeogeodesy.xls.
Great Circle - Chavin de Huantar	e-w @ Puma Punku = 1.0 : 1.61801
Newark Octagon - Pachacamac	e-w @ Poverty Point = 1.0 : 1.61810
Castillo - Observatory Circle	e-w @ Huayna Picchu = 1.0 : 1.61803
Castillo - Octagon Gateway	e-w @ Machu Picchu Peak = 1.0 : 1.61804

Download the Google Earth file, Golden Mean Longitudes:  jqjacobs.net/kml/phi_golden_ratios.kml

Stated simply, the golden mean or golden ratio divides a line such that the whole is proportional to the longer part as the longer part is to the shorter part. The golden mean, x : 1 = 1 : x + 1, stated numerically is 0.618034. : 1.0 = 1.0 : 1.618034, where Phi like pi is an infinite irrational number (1.6180339887...). Upper case Phi is 1.618... and lower case phi is 0.618..., Phi - 1 = phi. I tend to ignore the Greek, italicized upper and lower case convention, refer to both in lower case, and reference the ratio moreso than the values. The formula obtains from a triangle with sides 2 : 1 and thus a hypotenuse equaling the square root of five. The values equate to half of two sides, [(the square root of five plus one) divided by two] and to [(square root of five minus one) divided by two]. The x - 1 = y and x + 1 = y formulations have relevance in the astronomy discussion below.

Chavin, Latitude Geometry, and Astronomy

An important astronomic and geodetic context for Chavin is latitude trigonometry. Chavin's latitude sine equals one-sixth (Figure 4). I previously discussed monument positioning at latitudes evidencing accurate astronomy and geodesy in Ancient Monument Latitudes Evidence Accurate Astronomy. The geometry of the angle between the local geodetic and the celestial reference frame presents a functional reason to place astronomical observatories at latitudes forming low-integer geodetic triangles. Monuments with small rational numbers describing local geodetic position have an astronomical practicality, considerable simplification of mathematical operations related to astronomy observations. With simple integer ratios expressing the triangular relationship of place to the axis of rotation and pole, complex and time consuming mathematical operations are reduced while also eliminating inaccuracy of decimal rounding. Additionally, the high elevation at Chavin is advantageous for doing astronomy observations.

Assuming intentional latitude placements, monument positioning manifests the earliest known capability of accurate latitude determination and the earliest known precise astronomical and geodetic measurements. Chavin's precise latitude placement alone implies Chavin was an astronomical observatory. The latitude with tangent one-sixth transects the nearby coastal Sechin Alto monument complex (Figure 5). The earliest monumental construction at Sechin Bajo, the western end of the Sechin monument complex, has been dated to 3500-3000 B.C.E, implying Andean astronomical observatories may predate pyramids in Egypt. The not-as-precise latitude placement of the Nabta Playa stone circle in Africa, near one-fourth the distance from equator to pole, could imply intentional latitude placemarking originated before 7,000 years ago.

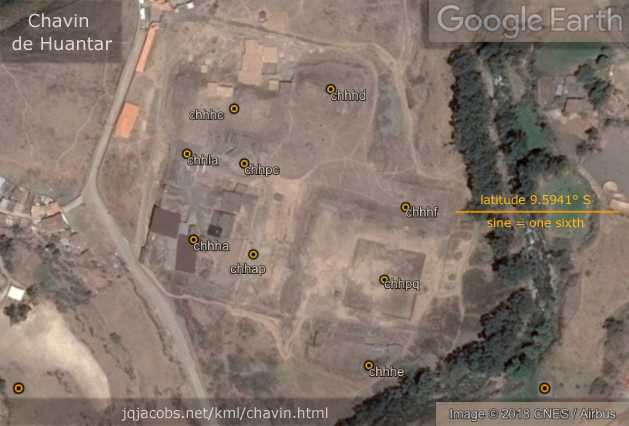
Figure 4. Chavin de Huantar latitude sine equals one-sixth.

Figure 5. Sechin Alto latitude tangent equals one-sixth.

Machu Picchu is framed by two astronomy constant baselines, to the north lunar orbit per rotation (0.036501 circumference, 13.140376°) and mean daily lunar motion (0.036601 circumference, 13.176352°) to the south near the summit of Cerro Machu Picchu (Figure 6). Huaca del Sol on the coast north of Chavin and Sechin, the largest ancient adobe structure in the Americas, is transected by the latitude with tangent equaling one-seventh (sol.kmz). At Monks Mound, the largest prehistoric monument north of Mexico and the largest-in-volume prehistoric earthen construction in the Americas, the latitude with tangent equaling four-fifths transects the mound.

Figure 6. The Machu Picchu and Llactapata latitude equates to a lunar orbit constant.

Chavin, Machu Picchu, and Nevado Illimani

Mountain peaks figure prominently in Andean culture to this day as well as in the archaeogeodesy study results. It is completely unsurprising that the highest mountains have a role in ancient geodesy; prominences in the landsape have an important role historically in surveying the earth. The Chavin to Machu Picchu arc distance equals the distance from Machu Picchu to Nevado Illimani (Figure 7). Also, the two arcs approximate a great circle line with the Chavin-Illimani direct line passing between Cerro Machu Picchu and the Intihuatana. Illimani at 6,438 m is the second highest peak in the Cordillera Real, east and south of the Lake Titicaca basin in Bolivia and Peru. The highest at 6,542 m, the dormant Nevado Sajama stratovolcano, has noteworthy archaeology in the complex of ancient lines between peaks in the surrounding area. During a flight from Santiago to La Paz, I was surprised witnessing them from 10,000 m and impressed by the vastness and sheer number of the lines.

Only two Peruvian peaks are higher than Illimani, 6,634 m Yerupaja and 6,768 m Huascaran near Chavin and Sechin. At Nevado Huascaran, the arcs ratio to Tikal and Denali, North America's highest peak, expresses the ratio one to pi. The longitude and latitude relationships of Chavin and Tikal to Aconcagua in Chile, the highest western hemisphere peak, are also significant.

Figure 7. Chavin and Nevado Illimani are equidistant from Machu Picchu.

Chavin, Pachacamac, Newark Earthworks, and Lunar Standstill

I initially discussed, in 2011 before publishing the phi longitude results, the relationships between Chavin, Pachacamac, Newark Earthworks, and lunar astronomy. In a 2009 log in the same webpage, Newark Archaeogeodesy, Assessing Evidence of Geospatial Intelligence in the Americas, I cited the relationships of Newark Earthworks to Tikal, Chichen Itza, and Pachacamac. These major sites have Chavin relationships expressing pi, phi, astronomy constants, and astrogeodetic modules. The mathematical expressions are often the spatial relationship of three monuments and the same proportions are expressed redundantly by various combinations of and different geometric relationships of the same major monuments. I find these to be strikingly impressive achievements of not only nesting the monumental arrangement on the spherical earth but also of both understanding fundamental cosmic motions and accurately determining the corresponding astronomical constants.

As with monument latitudes evidencing the earliest known observatories, the site inter-relationships imply the earliest-known precise knowledge of astronomical constants, both new findings to science. The advanced astronomical understandings expressed by these ancient monuments eclipses even modern astronomy by prioritizing sidereal (heliocentric, fixed-space) values, in sharp contrast to the geocentric bias of Western astronomy. The lunar astronomy constants expressed redundantly by the Chavin, Pachacamac, and Newark Earthworks arcs, arc distance ratios, and latitude differences (Figure 8, Chavin epoch UT values) are the product of a lunar motion, rotation of the inclination of lunar orbit. Lunar orbit inclination rotating on its axis determines the position of nodal intersection of lunar and solar orbit planes and thus the periodicity of eclipses. The same motion combined with precession of earth's rotation axis results in the lunar standstill period.

Western astronomy is focused on the apparent 18.612 year period of the varying angular span of moonrises and moonsets on the horizon. The 18.599 year sidereal cycle correlated to lunar motion, the predominant constant expressed by the monuments, corresponds to the lunar node retrograde rotation around the ecliptic, the effect of lunar orbit inclination turning and slowly gyrating where eclipses occur in relation to fixed space. Ancient monuments evidencing both precisely, the 18.599 year motion cycle and the 18.612 year period, implies advanced understanding of lunar motions and precession. The longitude difference between Chavin's Circular Plaza, Chichen Itza Castillo, and the centerpoints of the Newark Octagon and Observatory Circle express both these astronomy values with precision, albeit with a shift in decimal position (Figure 8).

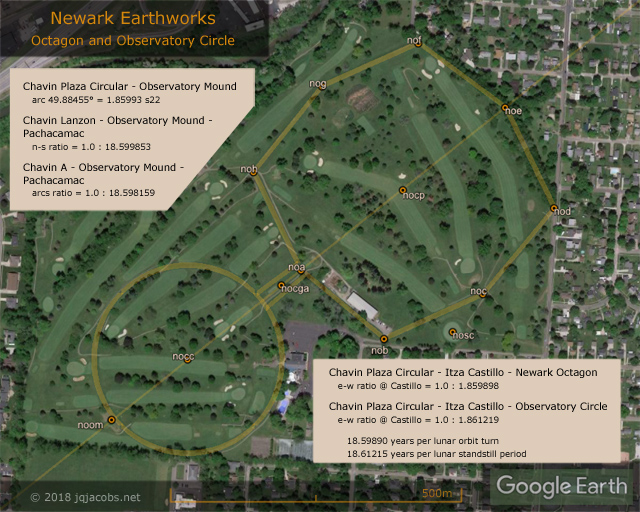
Figure 8. Newark Earthworks, Chavin, Pachacamac, Chichen Itza, and Lunar Major Astronomy.

If precision within a few meters (the margin of error in the coordinates of my GPS readings) relative to inter-continental arc distances (one part in one million) along with using epoch adjusted constants in Universal Time (UT) with the precision of advanced present-day astronomy isn't evidence enough, the arc distances ratio from Chichen Itza to Newark and to Machu Picchu repeat the same numbers. And the specific monument triad most accurately expressing lunar standstill is also the triad expressing the phi longitudes with precision (Figure 9).

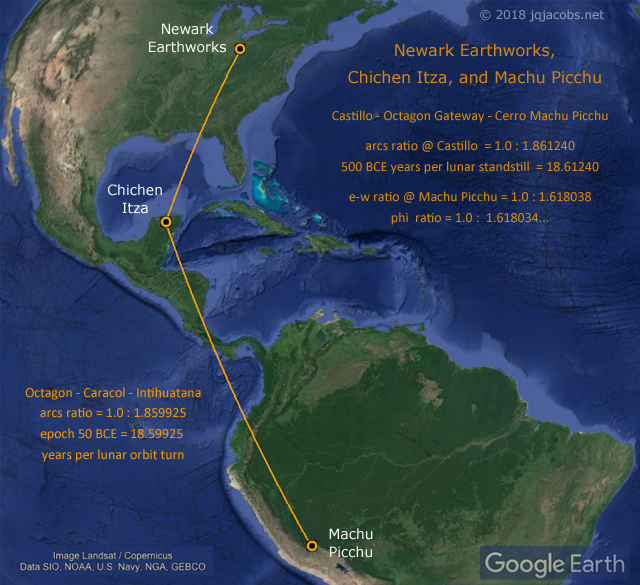
Figure 9. Newark Octagon, Chichen Itza, Machu Picchu, and Lunar Orbit Motion.

Adding to the redundancy are factors of the astrogeodetic module s22 expressed by the same sites as discussed in previous posts. The module s22 is degrees of solar orbit between lunar nodal crossings, a harmonic of eclipses. The arcs ratios from Chavin to Newark expresses the lunar constant as an s22 value (Figure 8), the 49.884546° arc from Chavin Plaza Circular to Observatory Mound equals 1.859934 s22 (Figure 10). The 2.68216° arc from Chavin Portal to Pachacamac equals 0.100004 s22, and the three sites are roughly a straight line, the line extending from Newark to Pachacamac passes 2.5 km east of Chavin. Thus, their n-s ratio and the arcs ratio repeat the number twice more. The n-s ratio at Chavin Lanzon to Pachacamac and Newark's Observatory Mound equals 1.0 to 18.59985. From Chavin A, the Pachacamac and Observatory Circle arcs ratio is 1.0 to 18.598159. At Pachacamac the ratio is 1.0 to 19.59812, the number of times the sun, earth and nodal crossing align per lunar orbit turn, once more than solar orbits during the cycle. The arc from Pachacamac to Observatory Mound equals 1.959957 s22. Arcs from Chavin to Caral and to Aspero, 0.050 s22, equal half the distance from Chavin to Pachacamac. Other s22 results in the placemarks file reinforce the import of nodal crossings in sidereal astronomy.

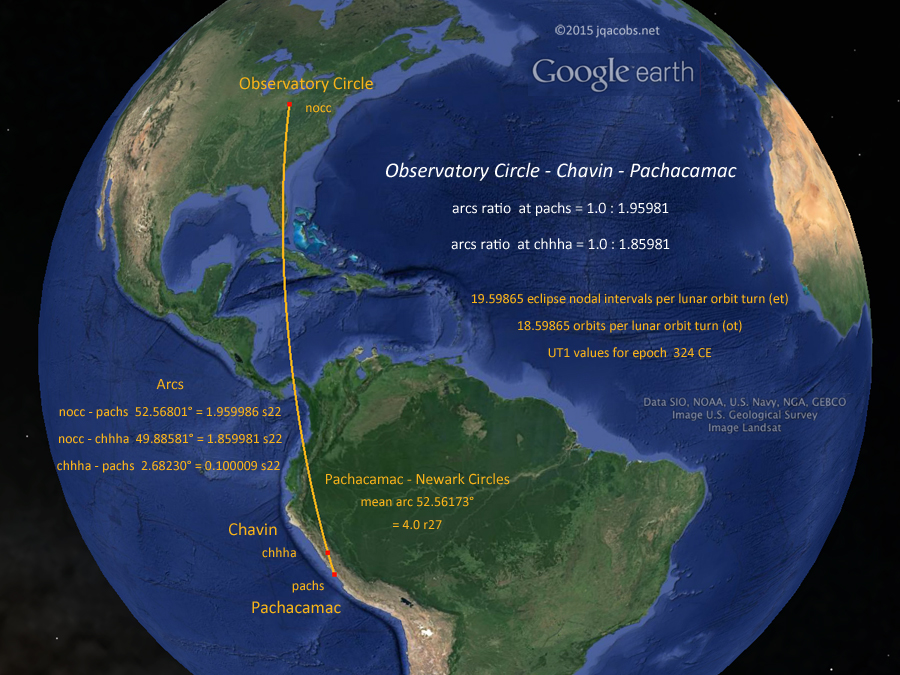
Figure 10. Chavin, Newark, and Pachacamac.

To add yet again to the redundancy, the years per lunar orbit turn numerical string repeats precisely with the latitudes ratio of Chavin, Caral, and Tiwanaku, this time with another shift in the decimal position (Figure 11). The Chavin to Tiwanaku arc transects 5,991 m Pumasillo, the second highest peak in the Cordillera Vilcabamba near Machu Picchu. The highest Cordillera Vilcabamba summit, 6,279 m Salkantay directly south of Machu Picchu, is the second highest prominence in Peru (after Huascaran) rising 2,540 m above the surrounding topography. The Chavin, Salkantay, and Pachacamac arcs ratio at Salkantay presents the solar orbits per lunar nodal period ratio. The Chavin, Salkantay, and Tumi Chucua arcs ratio at Chavin presents the orbits per lunar standstill period ratio. Tumi Chucua Zanja, the immense Amazonian circle expressing a pi relationship with 321 m Observatory Circle at Newark, is positioned 0.10 radians from Illimani and 0.10 diameters from Huascaran, albeit these two geodetic arcs are less precise than the previously cited astronomical arcs (see Tumichucua, Newark, and Pi: tumichucua.kml).

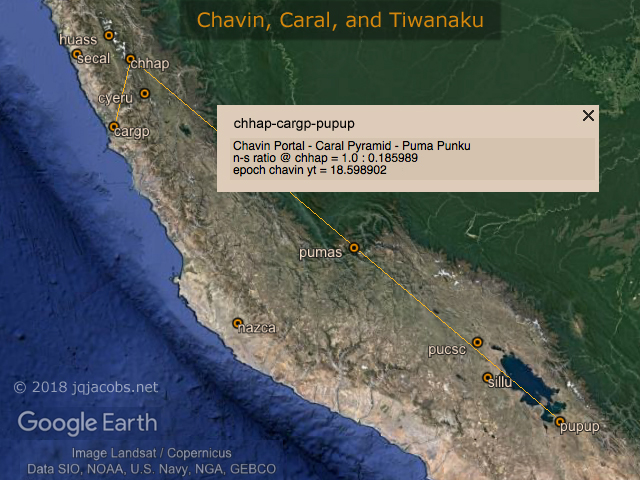
Figure 11. Chavin, Caral, Nazca, and Tiwanaku latitudes.

Astronomy Fundamentals

Understanding astronomy is a prerequisite to comprehending the significance of ancient monument relationships. Needless to say, no one told me I needed an advanced understanding of astronomy to do archaeology or that archaeology can advance understanding astronomy. I was interested in both sciences before realizing they combined. Eventually I recognized a necessity to present astronomy from a new perspective, one more aligned with the sidereal astronomy revealed by the monument research. My fundamental astronomy primer in Eclipses, Cosmic Clockwork of the Ancients provides such a cosmic context. The following discussion, much terser essentials, is context for the Chavin study results discussed herein. First, an excerpt:

Lunar major and lunar minor standstills describe the variable extent of lunar declination each nodal period, visible as the moon swinging every 27.2122 mean days from high in the sky and rising north of east to low in the sky and rising south of east. Full moons nearest solstices during major standstill add lunar inclination to earth's axis inclination while at mid-cycle 9.3 years later on the opposite side of the sun lunar orbit inclination subtracts. Before artificial lighting, how bright the moon lit nights was corresponded to the nodal period and, less so, to the 18.612 year standstill period. Newark's Octagon and Observatory Circle align to the northern extrema lunar major moonrise (Figure 8) every 18.6 years.

Knowlege of sidereal astronomy, orbits and rotation in fixed space, is an inherent understanding in the astronomy constants expressed by the monument relationships. One fundamental astronomical ratio, rotations per lunar orbit, is both very significant in the archaeology results and readily observable by naked eye astronomy. With sufficient temporal observation the ratio of these two sidereal motions is easily determined with precision. Decades ago I noticed the 500 A.D. Indian book on astronomy, The Àryabhatiya of Àryabhata, evidences an accurate ratio of earth rotations and lunar orbits. An even earlier recognition and awareness of accurate, heliocentric cosmology is implied by the precise astronomy constants (Table 2) expressed by the the arrangement of ancient monuments.

There came a point when I realized apparent ancient knowledge exceeded contemporary understanding of how to determine the knowledge. Forced to consider how their achievements could be accomplished and vexed by knowing a solution must exist, I finally overcame present-day paradigms and biases and arrived at an elegantly simple solution, one which should have been apparent all along to myself and Western astronomy. This astronomical reasoning exercise repeated my geodetic experience with longitude determination. Solving longitude is far easier with fewer unknowns, likewise with astronomy. On land, time and place are not unknown so longitude determination is simplified, plus you are not drifting on a ship so you can take centuries to refine accuracy from a fixed position such as at Chavin's known latitude. With heliocentric astronomy, rotation and orbits are not unknowns and thus resolving astronomy constants is straightforward, was possible thousands of years ago, and with centuries of observations can achieve precision. Geocentrism obfuscates earth's rotation and thus the key ratio of lunar orbits per rotation (0.036501 circumference) and the solution.

How precise astronomy constants were accessible to ancient astronomers can be summarized in one paragraph. Eclipses enable precisely observing the ratio of lunar synodic to lunar orbits. Using a short term example, just one Metonic eclipse cycle (Table 3), with 254 lunar orbits equating with 235.000467 synodic periods, 18.999533 fewer moons, we can deduce that 18.999533 solar orbits have completed during 254 lunar orbits and by division arrive at 13.368750 lunar orbits per solar orbit (Chavin epoch UT values, 0.0748013 solar orbits per lunar orbit). From a tally of earth rotations in 254 lunar orbits, the value of rotations per solar orbit easily computes, with 6958.703831 divided by 18.999533 equaling 366.256576. Solving rotations per orbit resolves all three fundamental motions and knowing there is one less day than rotation per orbit allows deducing the number of days per orbit.

I presented the solution in Ancient Astronomy, Integers, Great Ratios, and Aristarchus, along with the indication historical ancient astronomers likely knew this. Integral to the solution is understanding the x - 1 = y geometry of orbital motion. From our geocentric perspective, unlike the precession determined year length, the solar orbit cycle is not easily quantified but is revealed by the x - 1 = y theorem. At the same instant that there is one less day than rotations there is also one less moon than lunar orbits due to the fact that one solar orbit has completed (Table 4). Understanding this theorem allows deducing 18.9995 solar orbits equates with 6,958.7038 rotations in the example above. (See also in the article, a longer term example, the 345-year eclipse interval.)

Counting in combination with the x - 1 = y geometry theorem solves the astronomy constants conumdrum, a simple solution which evaded archaeoastronomy and went unnoticed by historical astronomy. The same method, using lunar motion, allows resolving other astronomy questions including the rate of precession of earth's axis. The lunar motion metric is 350,000 times more accurate than direct measure of precession (epoch chavin lp = 349,219 lunar orbits per precession cycle). With the 345-year eclipse interval, nearly five days after 345 years, 345 orbits complete and the eclipse of full moon number 4,267 occurs half-a-day before 4,612 lunar orbits complete. The difference between years and orbits is precession quantified and earth rotations, lunar eclipses, and lunar orbits are the metrics.

In the case of precession, the theorem is instead x + 1 = y (Table 2) because the motions are opposing. For example, there is one more eclipse nodal interval than solar orbits per lunar orbit turn. Solving precession resolves the difficult to directly observe period of lunar standstill in relation to lunar orbit turning. Knowledge of both quantities is demonstrated with the longitude ratios of the Itza Castillo and Chavin's Old Temple circular plaza to the centerpoints of the Octagon and Observatory Circle (Figure 8). These are repeated with the relationships of Machu Picchu, Chichen Itza, and Newark (Figure 9). And the knowledge is precisely quantified redundantly in the relationships of Newark, Chavin and Pachacamac (Figure 10). Not only wouldn't the configuration be achieved without knowledge of the astronomy, knowledge of the full complexity of the cosmic motions and their relative significance is demonstrated.

Ancient Monuments and Lunar Orbits per Rotation

Earth's rotation on its axis is the precise clock, a steadfast motion accurately subdivided and counted using stellar positions. The moon's motions are complex and the lunar orbit is elliptical. Long periods of observation smooth lunar inconsistency plus understanding lunar orbit geometry allows determining observation intervals of greatest accuracy. The importance of an accurate, observable fundamental motion ratio is apparent in the solution in Table 3. This 0.036501 lunar orbits per rotation ratio occurs in the Chavin archaeogeodesy results. The n-s ratio from Poverty Point Earthworks to Chavin and to Tikal is 1.0 : 0.365009. At Aconcagua the e-w ratio to Chavin Portal and Tikal IV is 1.0 : 0.365015. The mean arc distance from Pachacamac to the Newark circles is four times 0.036501 circumference (4.0 r27).

The 1.0 : 0.036501 ratio repeats in the relationships of other major sites. At Monks Mound, the arcs to Tikal and Tiwanaku express the numerical string (Figure 12). The arcs ratio from Marcahuamachuco Castillo to Sechin Alto and to Pachacamac is 1.0 : 0.365004, and at Marcahuamachuco Monjas 1.0 : 0.366001, reflecting both lunar orbits per rotation and per day. Machu Picchu is situated between 0.036501 and 0.036601 circumferences south of the equator. Arc distance from the Intihuatana to Teotihuacan's Pyramid del Sol equals 0.3650130 diameters, and from Huayna Picchi Peak to Piramide de la Luna 0.365018 diameters. From the Sun Pyramid the arcs ratio to Huayna Picchi Peak and the Mut Temple at Karnak, Egypt, equals 1.0 : 0.365018. Mut in Egyptian mythology is the sky goddess mother of Khonsu, the god of the moon. Way back in 1991 before I had the tools to determine accuracy, I noticed the arc distance from Karnak, Egypt, to the great pyramids in the Americas, Teotihuacan and Cholula, closely approximates circumference divided by pi, the diameter of the earth.

Arcs today from the Second Pylon entrance of Karnak's Great Hypostyle Hall to Teotihuacan's Piramide de la Luna and to the Cholula Pyramid average 114.59147° or circumference divided by 3.1415951, within 10 meters of expressing pi precisely. From Machu Picchu Torreon the Tikal III and Karnak Luxor Pylon arcs precisely express the ratio one to pi. At Teotihuacan's Quetzalcoatl Pyramid the e-w ratio to the Intihuatana and to Karnak's Mut Temple is 1.0 : 0.200001. Spanning the Atlantic makes plate tectonics a significant variable in considering accuracy. And the older the monuments the greater the tectonic motion factor in considering accuracy of present relationships. I include a tectonics folder in the KML file modeling Chavin's motion since the Neolithic, about the time the Giza pyramids were built (east of Chavin 108.31 degrees, cosine = -0.314159).

With the Teotihuacan, Machu Picchu, Karnak triad of monumental sites another utility of shifting decimals is noted, expressing several very different constant values. From the Moon Pyramid the arcs ratio to Cerro Machu Picchi and to the Hypostyle Hall equals 1.0 : 0.365236. Even though 365.24 and 0.003650 are very different numbers, with the decimals shifted both are represented in ratios presented by the same three monument complexes.

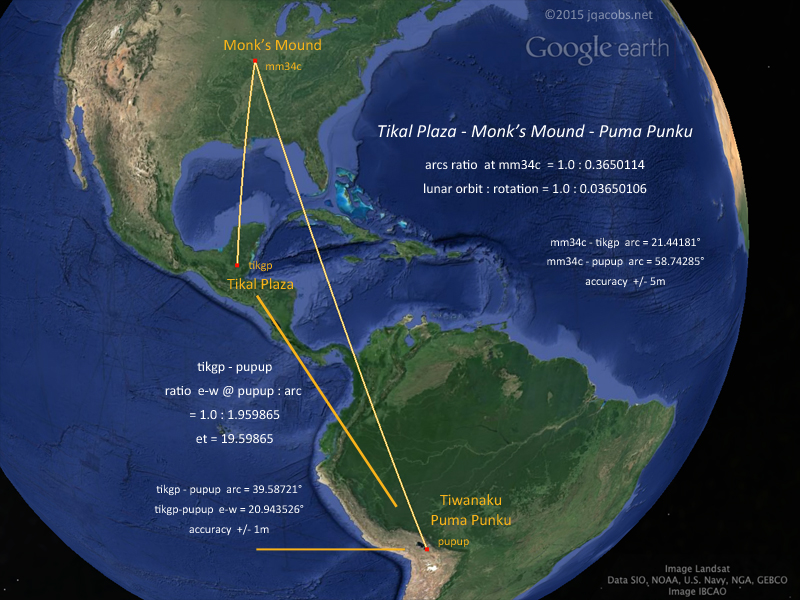
Figure 12. Tikal, Cahokia, and Tiwanaku.

At Chavin Plaza the arcs ratio to 34 m tall La Venta Pyramid Mound in Mexico and to 40 m tall Silbury Hill in Great Britain is 1.0 : 0.3650104, arcs over 3.5 million and 9.8 million meters long with a ratio inaccuracy of -1.5 m. These two long arcs are a particularly good example of how shifting the decimal position (one lunar orbit : ten rotations) facilitates expressing the ratio accurately, accurate to within one part in two and one-third million instead of one-tenth that vast length. From Pachacamac to Mohenjo-daro presents an even longer arc distance, 0.40 circumference. So with the Pachacamac to Newark arc equaling 4.0 r27 (4 times 0.03650 circumference), at Pachacamac the arcs ratio to Observatory Mound and to Mohenjo-daro East Town is 1.0 : 0.36501075. The Newark to Mohenjo-daro arc is 4 s22, so from Mohenjo-daro the arcs express the ratio of orbits per lunar nodal period, the s22 module (0.40 circumference : 4 s22 = 1.0 : 10 s22 = 1.0 : 0.7450). This is also the arcs ratio from Salkantay to Chavin and to Pachacamac. From Newark the ratio expressed is lunar orbit per rotation to solar orbit per lunar nodal period (4 r27 : 4 s22).

Chavin and the Origins of Civilization

The placements and arrangement of the monuments discussed above cannot be written off as coincidence. The earth is so large in scale and given so many precise relationships, the most significant question posed by the results, intentionality, answers itself. Accepting the results as a valid aspect of past civilization in the Americas and elsewhere shatters paradigms and generates many new questions for archaeology. Human intellectual history is rewritten by this ancient codex on the earth. The question of who we are as humans has new context. I'll leave the philosophical questions and implications for another time and contextualize an important archaeology question for now. Where and when did ancient geodesy originate?

How to arrive at a satisfactory answer is a challenging puzzle? The relationships of monuments and mountains provides a deductive tool, mountains came first. Huascaran, Aconcagua, Illimani, Salkantay, Denali, Cerro Machu Picchu, et.al., all are fixed points, enduring geodetic references. Contrastingly, many points share the latitude of Chavin, or Sechin and others, offering flexibility in placements at specific latitudes. Dating of archaeological sites also frames questions with differing threshold dates. Site origin may be older than a monumental construct, but at least dating a monument provides a specific time depth, a minimum age for a placemark.

The longitude difference between Giza and Chavin, 108.310° e-w, has a cosine value of -0.314159. The two Chavin placemarks in the lower right and left corners of Figure 4 are 108.310067° (cosine = -0.314159) west of Khufu's pyramid and Khafre's pyramid respectively. This could be written off as coincidence were it not for other relationships, especially when the Giza and Newark e-w cosine is -0.40. Not only is the ratio pi to 4.0 significant, the other Chavin and Newark relationships are supportive context also. At Newark today, 113.578178° (cosine = -0.40) west of Khufu's pyramid is 32 meters from the centerpoint of the 1,700 meter plus Octagon. The longitude difference cosines from the Octagon and from Chavin Plaza to Khufu Pyramid have a ratio of -0.400005 to -0.314178. From 2006 in Temporal Epoch Calculations:

Chavin is dated more recent than the great pyramids, so if Giza was point positioned first, the placement of an observatory in the high Andes at Chavin's latitude west 108.310° determined Chavin's longitude. Chavin couldn't be placed elsewhere on the same latitude given this e-w criteria and the Octagon's longitude would be likewise fixed. Given Chavin's fixed latitude, Newark's latitude is determined by the relationships to Chavin. This scenario fits known dates and illustrates possible deductions regarding origin and sequence. Along with mountain positions, certain givens can foreclose other possibilities. Mountains with results in relation to Giza, Chavin, and major sites may restrict the plausible sequence of monuments—after all the mountains precede the monuments.

My coordinates representing mountains and monuments have variable margins of error. The GPS readings at Newark and elsewhere are within 5 meters and their accuracy is stated in the archaeogeodesy.xls sites database where all coordinate sources and known GPS accuracies are specified. Coordinates determined from Google Earth (GE) may be less precise, vary in accuracy, and their margins of error are not defined. The GE coordinates have vastly improved over time with higher resolution imagery updates. I address and illustrate this in the Chaco Meridian article where different GE satellite images are overlayed with my Southwest GPS survey data. Deriving mountain peak coordinates from satellite topography data is even less accurate than photographic, pixel-scale differentiation.

I cannot find GPS data for Nevado Tarata, a pyramidal peak and the highest point in one of Peru's twenty cordilleras displaced just 3.5 kilometers from the direct line between Chavin and Machu Picchu. I doubt a GPS reading exists since the remote peak has rarely been conquered. From Tarata to Chavin and to Machu Picchu the arcs ratio is 1.0 to 0.365013, accurate to one part in 100,000 with an uncertain margin of error. I initially considered Salkantay with coordinates of unknown precision. Recently Nate Heald obtained Salkantay GPS data for the east summit. I lack GPS data for Salkantay's western summit which was 30m higher before a collapse in the 1970s. While the mountains do predate the monuments, they can change with time. Using Nate's GPS data for the east summit, fuzzy preliminary Salkantay results shifted to precise relationships.

At Salkantay due south of Machu Picchu, the Teotihuacan and Karnak e-w ratio of course repeats. Center-on-center, from the Moon Pyramid the longitude ratio to Salkantay and to Karnak's Temple of Amun Re is 1.0 : 0.200000. From the Sun Pyramid the longitude ratio to Salkantay and to Karnak's Hypostyle Hall is 1.0 : 0.200000. The Karnak temple complex spans about 320 m east-west and these are the two buildings along the primary axis. From the Sun Pyramid the arcs ratio to Salkantay and the Temple of Amun Re is 1.0 : 0.366243. Epoch Chavin rotations per year equals 366.242556. The arc distance from Salkantay to the Moon Pyramid equals 0.366240 diameters. Salkantay also has accurate relationships with Newark Earthworks and other monuments outside the scope of this discussion.

Karnak and Teotihuacan relationships with Cerro Machu Picchu and Huayna Picchu are noted above. The three mountains are fixed points which existed before the monuments. The Intihuatana is also a fixed peak, carved bedrock atop a prominence amidst the ancient walls and terraces. Salkantay is more significant in the Chavin results than higher Huascaran near Chavin. Which monument existed first, Chavin or Machu Picchu? The walls at Machu Picchu may not be old compared to Chavin. Did Inca construction honor a far older site heritage? What of the great pyramids, the Stones of Stennes, the ancient passage mounds at Carrowkeel, are these all part of a cultural tradition as old as the stone placements at Nabta Playa?

Andean mountain peaks are a foundation for key monument placements. The mountains contextualize the question of where and when ancient geodesy originated. The challenging puzzle of the origins of ancient geodesy and advanced civilization brings very different and surprising perspectives to current understandings of archaeology and the unity of past civilizations. The monuments and mountains taken together continue to provide surprising answers to "Where and when did ancient geodesy originate?" as well as to many other questions.

Afterword

Even more Chavin results are presented in the placemarks file. Archaeogeodesy study results for other sites are presented in KML files linked above and below and the results discussed herein should be considered in this larger context. Also, my research applet is linked below so professionals can delve into the subject on their own. Don't be surprised to "discover" more than I present online. Watch the ArchaeoBlog for resource updates and future articles. As I continue to research more accurate coordinates, details and deep decimals may be updated herein and in the KML files. Download current versions of all files for the most recent data.